已知：如图，在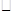
ABCD中，AE⊥BC，垂足为E，CE=CD，点F为CE的中点，点G为CD上的一点，连接DF、EG、AG，∠1=∠2。
（l）若CF=2，AE=3，求BE的长；
（2）求证：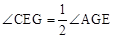
。
+2)÷
，其中
，
.
；（2）
；（2）
相关知识点
推荐套卷
已知：如图，在ABCD中，AE⊥BC，垂足为E，CE=CD，点F为CE的中点，点G为CD上的一点，连接DF、EG、AG，∠1=∠2。
（l）若CF=2，AE=3，求BE的长；
（2）求证：。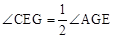
粤公网安备 44130202000953号