“4·20” 雅安地震后,某商家为支援灾区人民,计划捐赠帐篷16800顶,该商家备有2辆大货车、8辆小货车运送帐篷。计划大货车比小货车每辆每次多运帐篷200顶,大、小货车每天均运送一次。两天恰好运完。
(1)求大、小货车原计划每辆每次各运送帐篷多少顶?
(2)因地震导致路基受损,实际运送过程中,每辆大货车每次比原计划少运200m顶,每辆小货车每次比原计划少运300顶,为了尽快将帐篷运送到灾区,大货车每天比原计划多跑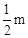 次,小货车每天比原计划多跑
次,小货车每天比原计划多跑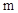 次,一天恰好运送了14400顶,求
次,一天恰好运送了14400顶,求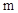 的值。
的值。
相关知识点
推荐套卷
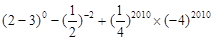 (2)
(2)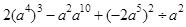
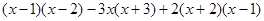 ,其中
,其中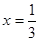
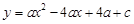 与x轴交于点A、点B,与y轴的正半轴交于点C,点 A的坐标为 (1, 0),OB=OC,抛物线的顶点为D.
与x轴交于点A、点B,与y轴的正半轴交于点C,点 A的坐标为 (1, 0),OB=OC,抛物线的顶点为D.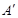 ,若
,若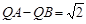 ,求点Q的坐标和此时△
,求点Q的坐标和此时△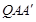 的面积.
的面积.
 ;
;
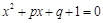 的一个实数根为 2.
的一个实数根为 2. 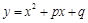 与x轴有两个交点;
与x轴有两个交点; 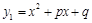 的顶点为M,与 y轴的交点为E,抛物线
的顶点为M,与 y轴的交点为E,抛物线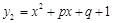
 ,PB=
,PB= ,PC=1,求∠BPC的度数.
,PC=1,求∠BPC的度数. ,PB=4,PC=2,则∠BPC的度数为,正六边形ABCDEF的边长为.
,PB=4,PC=2,则∠BPC的度数为,正六边形ABCDEF的边长为.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号