如图，AC 是圆 O 的直径，点 B 在圆 O 上，∠BAC＝30°，BM⊥AC交 AC 于点 M，EA⊥平面ABC，FC//EA，AC＝4，EA＝3，FC＝1．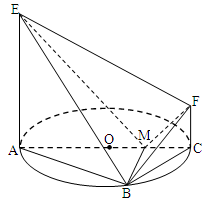
（I）证明：EM⊥BF；
（II）求平面 BEF 与平面ABC 所成锐二面角的余弦值．
，
}的前n项和为Sn，且
＝
的值域.
前n项的和。
时，求函数
的定义域；
的取值范围。推荐套卷
如图，AC 是圆 O 的直径，点 B 在圆 O 上，∠BAC＝30°，BM⊥AC交 AC 于点 M，EA⊥平面ABC，FC//EA，AC＝4，EA＝3，FC＝1．
（I）证明：EM⊥BF；
（II）求平面 BEF 与平面ABC 所成锐二面角的余弦值．
粤公网安备 44130202000953号