如图，在平面直角坐标系中，已知A（8，0），B（0，6），⊙M经过原点O及点A、B．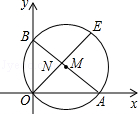
（1）求⊙M的半径及圆心M的坐标；
（2）过点B作⊙M的切线l，求直线l的解析式；
（3）∠BOA的平分线交AB于点N，交⊙M于点E，求点N的坐标和线段OE的长．
相关试题
王大伯几年前承包了甲、乙两片荒山，各栽100棵杨梅树，成活98%．现已挂果，经济效益初步显现，为了分析收成情况，他分别从两山上随意各采摘了4棵树上的杨梅，每棵的产量如折线统计图所示．
（1）分别计算甲、乙两山样本的平均数，并估算出甲、乙两山杨梅的产量总和；
（2）试通过计算说明，哪个山上的杨梅产量较稳定？
生活经验表明，靠墙摆放的梯子，当50°≤α≤70°时（α为梯子与地面所成的角），能够使人安全攀爬．现在有一长为6米的梯子AB，试求能够使人安全攀爬时，梯子的顶端能达到的最大高度AC．
（结果保留两个有效数字，sin70°≈0.94，sin50°≈0.77，cos70°≈0.34，cos50°≈0.64）
．如图，在平面直角坐标系中，已知点A（0,2），点P是x轴上一动点，以线段AP为一边，在其一侧作等边三角线APQ。当点P运动到原点O处时，记Q得位置为B。
（1）求点B的坐标；
（2）求证：当点P在x轴上运动（P不与Q重合）时，∠ABQ为定值；
（3）是否存在点P，使得以A、O、Q、B为顶点的四边形是梯形？若存在，请求出P点的坐标；若不存在，请说明理由。
，令y=0，可得x=1，我们就说1是函数
(
m为常数)。
和
，且
，此时函数图象与x轴的交点分
上，当MA+MB最小时，求直线AM的函数解析式。推荐套卷
粤公网安备 44130202000953号