一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,篮球1个,黄球若干个,现从中任意摸出一个球是红球的概率为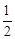 .
.
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,求两次摸出都是红球的概率;
(3)现规定:摸到红球得5分,摸到黄球得3分(每次摸后放回),乙同学在一次摸球游戏中,第一次随机摸到一个红球第二次又随机摸到一个蓝球,若随机,再摸一次,求乙同学三次摸球所得分数之和不低于10分的概率.
相关知识点
推荐套卷


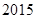 年
年 月
月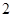 日云南临沧沧源发生
日云南临沧沧源发生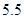 级地震,牵动着全国人民的心,地震后某中学举行了爱心捐款活动,下图是该校九年级某班学生为沧源灾区捐款情况绘制的不完整的条形统计图和扇形统计图.
级地震,牵动着全国人民的心,地震后某中学举行了爱心捐款活动,下图是该校九年级某班学生为沧源灾区捐款情况绘制的不完整的条形统计图和扇形统计图.
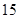 元人数”所在扇形的圆心角的度数;
元人数”所在扇形的圆心角的度数; 人,据此样本,请你估计该校九年级学生共捐款多少元?
人,据此样本,请你估计该校九年级学生共捐款多少元?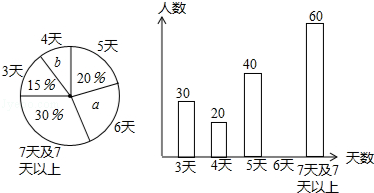

 粤公网安备 44130202000953号
粤公网安备 44130202000953号