阅读材料： 小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如：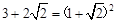
，善于思考的小明进行了以下探索：
设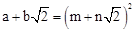
（其中
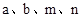均为整数），则有 
．
∴
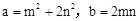．这样小明就找到了一种把部分
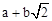的式子化为平方式的方法．
请你仿照小明的方法探索并解决下列问题：
当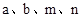均为正整数时，若
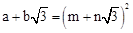，用含m、n的式子分别表示
，得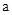 
＝ ，
＝ ；
（2）利用所探索的结论，找一组正整数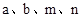，填空： ＋ ＝( ＋ 
)2；
（3）若
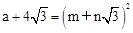，且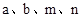均为正整数，求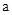的值．
相关试题
25、为了美化博望中学校园环境，建设绿色校园，我校准备对校园中30亩空地进行绿化．绿化采用种植草皮与种植树木两种方式，要求种植草皮与种植树木的面积都不少于10亩，并且种植草皮面积不少于种植树木面积的三分之二．已知种植草皮与种植树木每亩的费用分别为8000元与12000元．
（2）种植草皮的面积为多少时绿化总费用最低，最低费用为多少？
某校八年级学生小丽、小强和小红到某超市参加了社会实践活动，在活动中他们参与了某种水果的销售工作，已知该种水果的进价为8元／千克，下面是他们在活动结束后的对话：
小丽：如果以10元／千克的价格销售，那么每天可售出300千克．
小强：如果以13元／千克的价格销售，那么每天可获取利润750元．
小红：通过调查验证，我发现每天的销售量
（千克）与销售单价
（元）之间存在一次函数关系．求（千克）与（元）（
）的函数关系式；
，5），（
，3）．
相关知识点
推荐套卷
粤公网安备 44130202000953号