已知直线PD垂直平分⊙O的半径OA于点B，PD交⊙O于点C，D，PE是⊙O的切线，E为切点，连结AE，交CD于点F．
（1）若⊙O的半径为8，求CD的长；
（2）证明：PE=PF；
（3）若PF=13，sinA=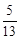
，求EF的长．
相关试题
在同一直线上，且
．求证：
．
，且
，
，
，求
和
的度数．
三等分，分点为
，过
作
的平行线，交
于点
，得多边形
，请用四个这样的小多边形，拼成一个形状相同的大多边形．
推荐套卷
已知直线PD垂直平分⊙O的半径OA于点B，PD交⊙O于点C，D，PE是⊙O的切线，E为切点，连结AE，交CD于点F．
（1）若⊙O的半径为8，求CD的长；
（2）证明：PE=PF；
（3）若PF=13，sinA=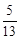，求EF的长．
粤公网安备 44130202000953号