如图，二次函数y=x2+bx－3b+3的图象与x轴交于A、B两点（点A在点B的左边），交y轴于点C，且经过点（b－2，2b2－5b－1）.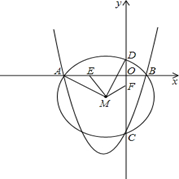
（1）求这条抛物线的解析式；
（2）⊙M过A、B、C三点，交y轴于另一点D，求点M的坐标；
（3）连接AM、DM，将∠AMD绕点M顺时针旋转，两边MA、MD与x轴、y轴分别交于点E、F，若△DMF为等腰三角形，求点E的坐标.
相关试题
如图，等边⊿ABC，点D、E分别在BC、AC上，且BD=CE，AD与BE相交于点F，
（1）试说明⊿ABD≌⊿BCE；
（2）⊿AEF与⊿ABE相似吗?说说你的理由；
（3）BD2=AD·DF吗?请说明理由．
已知抛物线过点A（－1，0），B（0，6），对称轴为直线x＝1
（1）求抛物线的解析式;
（2）画出抛物线的草图;
（3）根据图象回答：当x取何值时，y>0.
相关知识点
推荐套卷
粤公网安备 44130202000953号