“安全教育，警钟长鸣”，为此，某校随机抽取了九年级（1）班的学生对安全知识的了解情况进行了一次调查统计．图①和图②是通过数据收集后，绘制的两幅不完整的统计图．请你根据图中提供的信息，解答以下问题：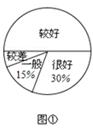
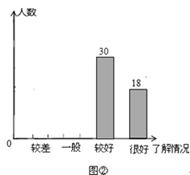
（1）九年级（1）班共有 名学生；
（2）在扇形统计图中，对安全知识的了解情况为“较差”部分所对应的圆心角的度数是 ；
（3）若全校有1500名学生，估计对安全知识的了解情况为“较差”、“一般”的学生共有 名．
如图1，小红家阳台上放置了一个晒衣架．如图2是晒衣架的侧面示意图，立杆AB．CD相交于点O，B．D两点立于地面，经测量：
AB=CD=136cm，OA=OC=51cm，OE=OF=34cm，现将晒衣架完全稳固张开，扣链EF成一条直线，且EF=32cm．
（1）求证：AC∥BD；
（2）求扣链EF与立杆AB的夹角∠OEF的度数（精确到0.1°）；
（3）小红的连衣裙穿在衣架后的总长度达到122cm，垂挂在晒衣架上是否会拖落到地面？请通过计算说明理由．
（参考数据：sin61.9°≈0.882，cos61.9°≈0.471，
tan61.9°≈0.553；可使用科学记算器）
我们约定：如果身高在选定标准的±2%范围之内都称为“普通身高”．为了了解某校九年级男生中具有“普遍身高”的人数，我们从该校九年级男生中随机抽出10名男生，分别测量出他们的身高（单位：cm），收集并整理如下统计表：
（1）计算这组数据的三个统计量：平均数、中位数、众数；
（2）请你选择其中一个统计量作为选定标准，找出这10名男生中具有“普遍身高”是哪几位男生？并说明理由．
小明的妈妈在菜市场买回3斤萝卜、2斤排骨，准备做萝卜排骨汤．
妈妈：“今天买这两样菜共花了45元，上月买同重量的这两样菜只要36元”；
爸爸：“报纸上说了萝卜的单价上涨50%，排骨单价上涨20%”；
小明：“爸爸、妈妈，我想知道今天买的萝卜和排骨的单价分别是多少？”
请你通过列方程（组）求解这天萝卜、排骨的单价（单位：元/斤）．
如图，等腰梯形ABCD放置在平面坐标系中，已知A（﹣2，0）、B（6，0）、D（0，3），反比例函数的图象经过点C．
（1）求点C的坐标和反比例函数的解析式；
（2）将等腰梯形ABCD向上平移2个单位后，问点B是否落在双曲线上？
粤公网安备 44130202000953号