(本小题满分13分)
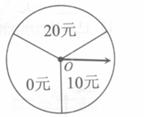
某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费每满100元可以转动如图所示的圆盘一次,其中O为圆心,且标有20元、10元、0元的三部分区域面积相等,假定指针停在任一位置都是等可能的.当指针停在某区域时,返相应金额的优惠券。(例如:某顾客消费了218元,第一次转动获得了20元,第二次获得了10元,则其共获得了30元优惠券。)顾客甲和乙都到商场进行了消费,并按照规则参与了活动.
(I)若顾客甲消费了128元,求他获得优惠券面额大于0元的概率?
(II)若顾客乙消费了280元,求他总共获得优惠券金额不低于20元的概率?