如图,过圆O外一点P作该圆的两条割线PAB和PCD,分别交圆 O于点A,B,C,D弦AD和BC交于Q点，割线PEF经过Q点交圆 O于点E、F，点M在EF上，且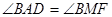
:
(I)求证:PA·PB=PM·PQ； (II)求证：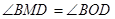
.
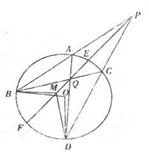
相关试题
中，
且
（
且
）．
为等差数列；
的前
项和
．
中，
平面
，
，
，
是
的中点，
是
上的点且
，
为△
边上的高．
平面
；
，
，
，求三棱锥
的体积；
中，角
、
、
所对的边分别为
、
、
，已知
，
，
．
的面积
；
．已知四棱锥P-ABCD，底面ABCD是
的菱形，又
，且PD=CD，点M、N分别是棱AD、PC的中点．
（Ⅰ）证明：DN//平面PMB；
（Ⅱ）证明：平面PMB
平面PAD；
推荐套卷
如图,过圆O外一点P作该圆的两条割线PAB和PCD,分别交圆 O于点A,B,C,D弦AD和BC交于Q点，割线PEF经过Q点交圆 O于点E、F，点M在EF上，且: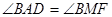
(I)求证:PA·PB=PM·PQ； (II)求证：.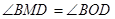
已知四棱锥P-ABCD，底面ABCD是的菱形，又，且PD=CD，点M、N分别是棱AD、PC的中点．
（Ⅰ）证明：DN//平面PMB；
（Ⅱ）证明：平面PMB平面PAD；
粤公网安备 44130202000953号