为了调查某大学学生在周日上网的时间，随机对1OO名男生和100名女生进行了不记 名的问卷调查.得到了如下的统计结果：
表1:男生上网时间与频数分布表
表2:女生上网时间与频数分布表
(I)若该大学共有女生750人,试估计其中上网时间不少于60分钟的人数；
(II)完成下面的2x2列联表，并回答能否有90%的把握认为“学生周日上网时间与性 别有关”？
表3：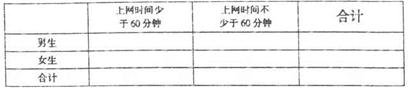
轴所得弦长为
；②被
轴分成两段圆弧，其弧长的比为
；③圆心到直线
：
的距离为
的圆的方程。
与已知圆
的交点，且在两坐标轴上的四个截距之和为8的圆的方程。
，且
，求
的值。
,求cosθ的值.推荐套卷
为了调查某大学学生在周日上网的时间，随机对1OO名男生和100名女生进行了不记 名的问卷调查.得到了如下的统计结果：
表1:男生上网时间与频数分布表
表2:女生上网时间与频数分布表
(I)若该大学共有女生750人,试估计其中上网时间不少于60分钟的人数；
(II)完成下面的2x2列联表，并回答能否有90%的把握认为“学生周日上网时间与性 别有关”？
表3：
粤公网安备 44130202000953号