如图，已知椭圆C：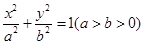 
的左、右焦点分别为
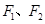，离心率为
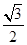，点A是椭圆上任一点，
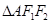的周长为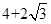
.
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点
任作一动直线l交椭圆C于
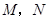两点，记
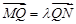，若在线段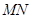
上取一点R，使得
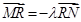，则当直线l转动时，点R在某一定直线上运动，求该定直线的方程.
，
是函数的一个周期。
，求
得取值范围，使函数
在区间
上是单调函数。
，若函数
的最大值为3，求实数m的值。
已知函数
的最小正周期相同，且
，(1)试确定
的单调增区间。
，求
的最值。推荐套卷
如图，已知椭圆C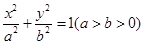： 的左、右焦点分别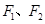为，离心率为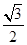，点A是椭圆上任一点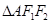，的周长为.
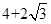（Ⅰ）求椭圆C的方程；
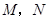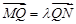（Ⅱ）过点任作一动直线l交椭圆C于两点，记，若在线段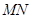上取一点R，使得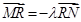，则当直线l转动时，点R在某一定直线上运动，求该定直线的方程.
粤公网安备 44130202000953号