已知函数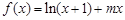
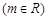 .
.
(Ⅰ)当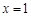 时,函数
时,函数 取得极大值,求实数
取得极大值,求实数 的值;
的值;
(Ⅱ)已知结论:若函数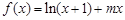
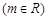 在区间
在区间 内存在导数,则存在
内存在导数,则存在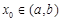 ,使得
,使得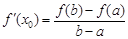 . 试用这个结论证明:若函数
. 试用这个结论证明:若函数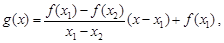 (其中
(其中 ),则对任意
),则对任意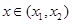 ,都有
,都有 ;
;
(Ⅲ)已知正数 满足
满足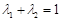 ,求证:对任意的实数
,求证:对任意的实数 ,若
,若 时,都
时,都
有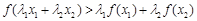 .
.
推荐套卷
已知函数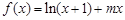
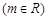 .
.
(Ⅰ)当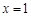 时,函数
时,函数 取得极大值,求实数
取得极大值,求实数 的值;
的值;
(Ⅱ)已知结论:若函数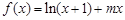
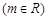 在区间
在区间 内存在导数,则存在
内存在导数,则存在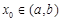 ,使得
,使得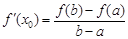 . 试用这个结论证明:若函数
. 试用这个结论证明:若函数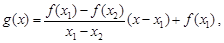 (其中
(其中 ),则对任意
),则对任意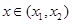 ,都有
,都有 ;
;
(Ⅲ)已知正数 满足
满足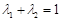 ,求证:对任意的实数
,求证:对任意的实数 ,若
,若 时,都
时,都
有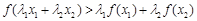 .
.