如图1，在梯形ABCD中，AB∥CD，∠B=90°，AB=2，CD=1，BC=m，P为线段BC上的一动点，且和B、C不重合，连接PA，过P作PE⊥PA交CD所在直线于E．设BP=x，CE=y．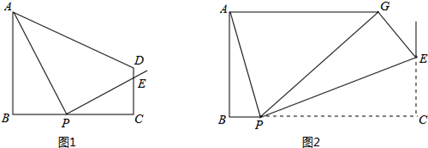
（1）求y与x的函数关系式；
（2）若点P在线段BC上运动时，点E总在线段CD上，求m的取值范围；
（3）如图2，若m=4，将△PEC沿PE翻折至△PEG位置，∠BAG=90°，求BP长．
的方程，形如
，使它的解在1到2之间；并把你编的方程解出来。相关知识点
推荐套卷
如图1，在梯形ABCD中，AB∥CD，∠B=90°，AB=2，CD=1，BC=m，P为线段BC上的一动点，且和B、C不重合，连接PA，过P作PE⊥PA交CD所在直线于E．设BP=x，CE=y．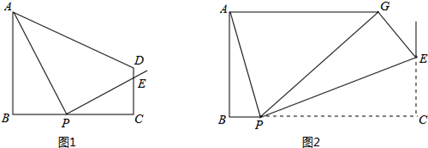
（1）求y与x的函数关系式；
（2）若点P在线段BC上运动时，点E总在线段CD上，求m的取值范围；
（3）如图2，若m=4，将△PEC沿PE翻折至△PEG位置，∠BAG=90°，求BP长．
粤公网安备 44130202000953号