如图，在梯形ABCD中，AB∥DC，∠B=90°，且AB=10，BC=6，CD=2．点E从点B出发沿BC方向运动，过点E作EF∥AD交边AB于点F．将△BEF沿EF所在的直线折叠得到△GEF，直线FG、EG分别交AD于点M、N，当EG过点D时，点E即停止运动．设BE=x，△GEF与梯形ABCD的重叠部分的面积为y．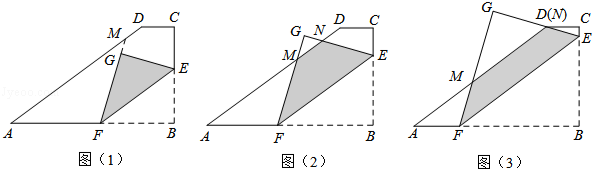
（1）证明△AMF是等腰三角形；
（2）当EG过点D时（如图（3）），求x的值；
（3）将y表示成x的函数，并求y的最大值．
相关试题
如图，在梯形ABCD中，AB∥DC，∠B=90°，且AB=10，BC=6，CD=2．点E从点B出发沿BC方向运动，过点E作EF∥AD交边AB于点F．将△BEF沿EF所在的直线折叠得到△GEF，直线FG、EG分别交AD于点M、N，当EG过点D时，点E即停止运动．设BE=x，△GEF与梯形ABCD的重叠部分的面积为y．
（1）证明△AMF是等腰三角形；
（2）当EG过点D时（如图（3）），求x的值；
（3）将y表示成x的函数，并求y的最大值．
中，
，
，
．若
，如图①，根据勾股定理，则
.若△
与
的关系，并证明你的结论．
三边长满足下列条件，判断△
;
.
是直线
上一点，
为任一条射线，
平分
，
平分
．
与
的补角；
与
具有怎样的数量关系．
，且
．
等于多少？
，求
互为相反数，
互为倒数，
的绝对值是
，求
的值．
粤公网安备 44130202000953号