如图,已知二次函数的图象过点A(0,﹣3),B( ),对称轴为直线
),对称轴为直线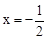 ,点P是抛物线上的一动点,过点P分别作PM⊥x轴于点M,PN⊥y轴于点N,在四边形PMON上分别截取PC=
,点P是抛物线上的一动点,过点P分别作PM⊥x轴于点M,PN⊥y轴于点N,在四边形PMON上分别截取PC= MP,MD=
MP,MD= OM,OE=
OM,OE= ON,NF=
ON,NF= NP.
NP.
(1)求此二次函数的解析式;
(2)求证:以C、D、E、F为顶点的四边形CDEF是平行四边形;
(3)在抛物线上是否存在这样的点P,使四边形CDEF为矩形?若存在,请求出所有符合条件的P点坐标;若不存在,请说明理由.
相关知识点
推荐套卷
 +
+ ,其中,a在1,2,
,其中,a在1,2, 这三个数中选取.
这三个数中选取. ;
;
 ).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的面四民﹒数学兴趣小组对捐款情况进行了抽样调查,速度分别为1,
).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的面四民﹒数学兴趣小组对捐款情况进行了抽样调查,速度分别为1, (长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
(长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
 与
与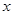 轴交于A、B两点(点A在点B的左侧),与
轴交于A、B两点(点A在点B的左侧),与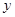 轴交于点C,点B的坐标为(3,0),将直线
轴交于点C,点B的坐标为(3,0),将直线 沿
沿
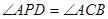 ,求点P的坐标.
,求点P的坐标. ,且OB边落在x轴的正半轴上,点A落在第一象限.将△OAB沿直线y=kx+b折叠,使点A落在x轴上,设点C是点A落在x轴上的对应点.
,且OB边落在x轴的正半轴上,点A落在第一象限.将△OAB沿直线y=kx+b折叠,使点A落在x轴上,设点C是点A落在x轴上的对应点.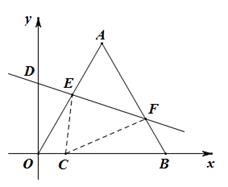
 时,点C的坐标。
时,点C的坐标。 粤公网安备 44130202000953号
粤公网安备 44130202000953号