阅读材料:
关于三角函数还有如下的公式: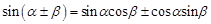
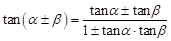
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值.
例: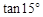
=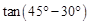
=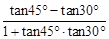
=
=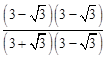
=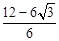 =
=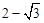
根据以上阅读材料,请选择适当的公式解答下面问题
(1)计算:sin15°;
(2)乌蒙铁塔是六盘水市标志性建筑物之一(图1),小华想用所学知识来测量该铁塔的高度,如图2,小华站在离塔底A距离7米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.62米,请帮助小华求出乌蒙铁塔的高度.(精确到0.1米,参考数据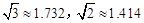 )
)
相关知识点
推荐套卷
 ÷ (
÷ ( -1),其中a=-1+
-1),其中a=-1+ .
. -(
-( )-1+(
)-1+(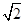 )0+
)0+ .
.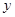 (元/米2)与楼层
(元/米2)与楼层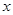 (2≤
(2≤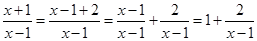 .
.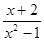
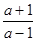
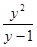
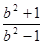
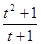 ,化成整式和真分式的和的形式.
,化成整式和真分式的和的形式. 粤公网安备 44130202000953号
粤公网安备 44130202000953号