如图，在直角坐标平面xOy中，抛物线C1的顶点为A(-1，4)，且过点B(-3，0)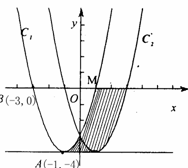 
(1)写出抛物线C1与x轴的另一个交点M的坐标；
(2)将抛物线C1向右平移2个单位得抛物线C2，求抛物线C2的解析式；
(3)写出阴影部分的面积S．
已知，正方形ABCD中，∠MAN="45°," ∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N，AH⊥MN于点H．如图①，当∠MAN绕点A旋转到BM=DN时，请你直接写出AH与AB的数
量关系： ；如图②，当∠MAN绕点A旋转到BM≠DN时，（1）中发现的AH与AB的数量关系还成立吗？如果不成立请写出理由．如果成立请证明；
如图③，已知∠MAN=45°，AH⊥MN于点H，且MH=2，NH=3，求AH的长．
（可利用（2）得到的结论） 
如图，已知抛物线C1：
的顶点为P，与x轴相交于A、B两点（点A在点B的左边），点A的横坐标是
．
求
点坐标及
的值；
如图（1），抛物线C2与抛物线C1关于x轴对称，将抛物线C2向左平移，平移后的抛物线记为C3，C3的顶点为M，当点P、M关于点A成中心对称时，求C3的解析式
；
如图（2），点Q是x轴负半轴上一动点，将抛物线C1绕点Q旋转180°后得到抛物线C4．抛物线C4的顶点为N，与x轴相交于E、F两点（点E在点F的左边），当以点P、N、E为顶点的三角形是直角三角形时，求顶点N的坐标．
已知：关于
的一元二次方程
（m为实数）若方程有两个不相等的实数根，求
的取值范围；在（1）的条件下，求证：无论
取何值，抛物线
总过轴上的一个固定点；若
是整数，且关于的一元二次方程有两个不相等的整数根，把抛物线向右平移3个单位长度，求平移后的解析式．
如图（1），凸四边形
，如果点
满足
，且
，则称点为四边形的一个半等角点．在图（2）正方形
内画一个半等角点，且满足
；在图（3）四边形
中画出一个半等角点，
保留画图痕迹（不需写出画法）．
粤公网安备 44130202000953号