如图，在平面直角坐标系中，坐标原点为O，A点坐标为（4，0），B点坐标为（﹣1，0），以AB的中点P为圆心，AB为直径作⊙P的正半轴交于点C．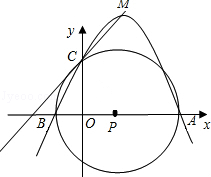
（1）求经过A、B、C三点的抛物线所对应的函数解析式；
（2）设M为（1）中抛物线的顶点，求直线MC对应的函数解析式；
（3）试说明直线MC与⊙P的位置关系，并证明你的结论．
相关试题
．如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A、B两点，A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，﹣3）点，点P是直线BC下方的抛物线上一动点．
（1）求这个二次函数的表达式．
（2）连接PO、PC，并把△POC沿CO翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．
（3）当点P运动到什么位置时，四边形ABPC的面积最大？求出此时P点的坐标和四边形ABPC的最大面积．
小明家所在居民楼的对面有一座大厦AB，AB=
米．为测量这座居民楼与大厦之间的距离，小明从自己家的窗户C处测得大厦顶部A的仰角为37°，大厦底部B的俯角为48°．求小明家所在居民楼与大厦的距离CD的长度．（结果保留整数）（参考数据：
）
相关知识点
推荐套卷
粤公网安备 44130202000953号