如图,等腰梯形ABCD中,AD∥BC,∠B=450,P是BC边上一点,△PAD的面积为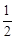 ,设AB=x,AD=y。
,设AB=x,AD=y。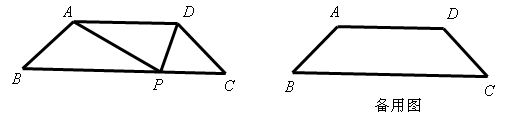
(1)求y与x的函数关系式;
(2)若∠APD=450,当y=1时,求PB·PC的值;
(3)若∠APD=900,求y的最小值。
推荐套卷
如图,等腰梯形ABCD中,AD∥BC,∠B=450,P是BC边上一点,△PAD的面积为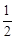 ,设AB=x,AD=y。
,设AB=x,AD=y。
(1)求y与x的函数关系式;
(2)若∠APD=450,当y=1时,求PB·PC的值;
(3)若∠APD=900,求y的最小值。