某校为了解该校九年级学生对蓝球、乒乓球、羽毛球、足球四种球类运动项目的喜爱情况，对九年级部分学生进行了随机抽样调查，每名学生必须且只能选择最喜爱的一项运动项目上，将调查结果统计后绘制成如图两幅不完整的统计图，请根据图中的信息，回答下列问题：
（1）这次被抽查的学生有 60 人；请补全条形统计图；
（2）在统计图2中，“乒乓球”对应扇形的圆心角是 144 度；
（3）若该校九年级共有480名学生，估计该校九年级最喜欢足球的学生约有 48 人．
相关试题
某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克．经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克.
（1）现该商场要保证每天盈利6000元，同时又要顾客得实惠，那么每千克应涨价多少元？
（2）若该商场单纯从经济角度看，每千克这种水果涨价多少元，能使商场获利最多？
已知：如图，二次函数
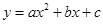的图象与x轴交于A、B两点，其中A点坐标为（-1，0），点C （0，5），另抛物线经过点（1，8），M为它的顶点.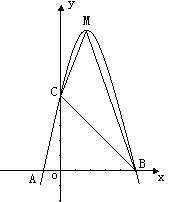
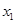（1）求抛物线的解析式；
（2）求△MCB的面积
.
已知：如图，AB是⊙O的直径，C、D为⊙O上两点，CF⊥AB于点F，CE⊥AD的延长线于点E，且 CE＝CF．
（1）求证：CE是⊙O的切线；
（2）若AD＝CD＝6，求四边形ABCD的面积．
，
是一元二次方程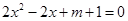
的两个实数根．
的取值范围；
，且
相关知识点
推荐套卷
粤公网安备 44130202000953号