如图，在平面直角坐标系xOy中，点A的坐标为（－2，0），等边三角形AOC经过平移或轴对称或旋转对称都可以得到△OBD。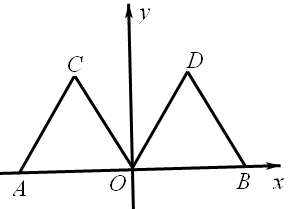
（1）△AOC沿x轴向右平移得到△OBD，则平移的距离是 个单位长度；△AOC与△OBD关于直线对称，则对称轴是 ；△AOC绕原点O顺时针旋转得到△OBD，则旋转角可以是 度；
（2）连接AD，交OC于点E，求∠AEO的度数。
在平面直角坐标系xOy中，抛物线
与y轴交于C点，与x轴交于A，B两点（点A在点B左侧），且点A的横坐标为-1．
（1）求a的值；
（2）设抛物线的顶点P关于原点的对称点为
，求点的坐标；
（3）将抛物线在A，B两点之间的部分（包括A， B两点），先向下平移3个单位，再向左平移m（
）个单位，平移后的图象记为图象G，若图象G与直线
无交点，求m的取值范围．
阅读、操作与探究：
小亮发现一种方法，可以借助某些直角三角形画矩形，使矩形邻边比的最简形式（如4：6的最简形式为2：3）为两个连续自然数的比，具体操作如下：
如图1，Rt△ABC中，BC，AC，AB的长分别为3，4，5，先以点B为圆心，线段BA的长为半径画弧，交CB的延长线于点D，再过D，A两点分别作AC，CD的平行线，交于点E．得到矩形ACDE，则矩形ACDE的邻边比为．
请仿照小亮的方法解决下列问题：
（1）如图2，已知Rt△FGH中，GH：GF：FH= 5：12：13，请你在图2中画一个矩形，使所画矩形邻边比的最简形式为两个连续自然数的比，并写出这个比值；
（2）若已知直角三角形的三边比为
（n为正整数），则所画矩形（邻边比的最简形式为两个连续自然数的比）的邻边比为．
如图，
是⊙
的直径，
是⊙上一点，
是
的中点，过点D作⊙O的切线，与AB，AC的延长线分别交于点E，F，连结AD．
（1）求证：AF⊥EF；
（2）若
，AB=5，求线段BE的长．
如图，平行四边形ABCD中，点E是AD边上一点，且 CE⊥BD于点F，将△DEC沿从D到A的方向平移，使点D与点A重合，点E平移后的点记为G．
（1）画出△DEC平移后的三角形；
（2）若BC=
，BD=6，CE=3，求AG的长．
的一元二次方程
有两个不相等的实数根．
的取值范围； 
粤公网安备 44130202000953号