我市某社区创建学习型社区,要调查社区居民双休日的学习状况,采用下列调查方式:
①从一幢高层住宅楼中选取200名居民;②从不同住宅楼中随机选取200名居民;③选取社区内200名在校学生。
⑴上述调查方式最合理的是 (填序号);
⑵将最合理的调查方式得到的数据制成扇形统计图和频数分布直方图,在这个调查中,200名居民双休日在家学习的有 人;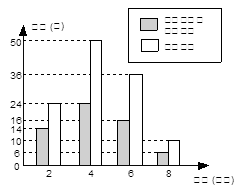
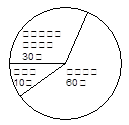
⑶请估计该社区2000名居民双休日学习时间不少于4小时的人数。
相关知识点
推荐套卷
我市某社区创建学习型社区,要调查社区居民双休日的学习状况,采用下列调查方式:
①从一幢高层住宅楼中选取200名居民;②从不同住宅楼中随机选取200名居民;③选取社区内200名在校学生。
⑴上述调查方式最合理的是 (填序号);
⑵将最合理的调查方式得到的数据制成扇形统计图和频数分布直方图,在这个调查中,200名居民双休日在家学习的有 人;
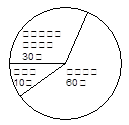
⑶请估计该社区2000名居民双休日学习时间不少于4小时的人数。