如图，四棱锥F－ABCD的底面ABCD是菱形，其对角线AC=2，BD=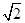
，AE、CF都与平面ABCD垂直，AE=1，CF=2.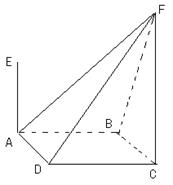
（I）求二面角B－AF－D的大小；
（II）求四棱锥E－ABCD与四棱锥F－ABCD公共部分的体积.
相关试题
中，内角
对边的长分别是
，且
.
，求
；
，求
中，角
的对边分别为
，向量
，
，且
；
的值；
，
，求角
的大小及向量
在
方向上的投影值.
是公差不为零的等差数列，
，且
是
和
的等比中项，求：
.
，
，（1）若
与
垂直，求
的值；（2）若
，求
中，
其前
项和
满足：
推荐套卷
如图，四棱锥F－ABCD的底面ABCD是菱形，其对角线AC=2，BD=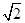，AE、CF都与平面ABCD垂直，AE=1，CF=2.
（I）求二面角B－AF－D的大小；
（II）求四棱锥E－ABCD与四棱锥F－ABCD公共部分的体积.
粤公网安备 44130202000953号