已知椭圆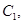
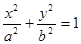(a>b>0)抛物线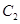
，从每条曲线上取两个点，将其坐标记录于下表中：
 |
 |
4 |
 |
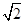1 |
 |
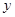2 |
4 |
 |
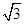2 |
（1）求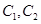
的标准方程；
（2）四边形ABCD的顶点在椭圆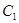
上，且对角线AC、BD过原点O，若
,
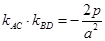(i) 求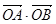
的最值.
(ii) 求四边形ABCD的面积；
相关试题
求函数
的最小值
，都有
有
的奇偶性；
时，
证明：
在
上为增函数；
，解不等式：
上是增函数命题q: 
恒成立。若p或q为真命题，命题p且q为假，
，B=
时，求
，求实数
的取值范围
的定义域为[-1，1]，求函数
+
的定义域推荐套卷
已知椭圆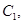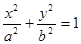(a>b>0)抛物线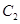，从每条曲线上取两个点，将其坐标记录于下表中：
|
|
4 |
|
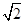1 |
|
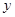2 |
4 |
|
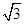2 |
（1）求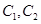的标准方程；
（2）四边形ABCD的顶点在椭圆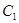上，且对角线AC、BD过原点O，若,
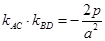(i) 求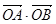的最值.
(ii) 求四边形ABCD的面积；
粤公网安备 44130202000953号