在平面直角坐标系 中,已知
中,已知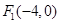 ,直线
,直线 , 动点
, 动点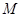 到
到 的距离是它到定直线
的距离是它到定直线 距离的
距离的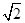 倍. 设动点
倍. 设动点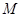 的轨迹曲线为
的轨迹曲线为 .
.
(1)求曲线 的轨迹方程.
的轨迹方程.
(2)设点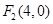 , 若直线
, 若直线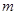 为曲线
为曲线 的任意一条切线,且点
的任意一条切线,且点 、
、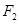 到
到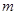 的距离分别为
的距离分别为 ,试判断
,试判断 是否为常数,请说明理由.
是否为常数,请说明理由.
推荐套卷
在平面直角坐标系 中,已知
中,已知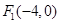 ,直线
,直线 , 动点
, 动点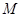 到
到 的距离是它到定直线
的距离是它到定直线 距离的
距离的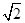 倍. 设动点
倍. 设动点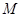 的轨迹曲线为
的轨迹曲线为 .
.
(1)求曲线 的轨迹方程.
的轨迹方程.
(2)设点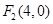 , 若直线
, 若直线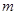 为曲线
为曲线 的任意一条切线,且点
的任意一条切线,且点 、
、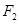 到
到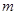 的距离分别为
的距离分别为 ,试判断
,试判断 是否为常数,请说明理由.
是否为常数,请说明理由.