“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度 (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度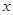 (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当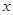 不超过4(尾/立方米)时,
不超过4(尾/立方米)时, 的值为
的值为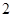 (千克/年);当
(千克/年);当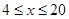 时,
时, 是
是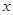 的一次函数;当
的一次函数;当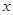 达到
达到 (尾/立方米)时,因缺氧等原因,
(尾/立方米)时,因缺氧等原因, 的值为
的值为 (千克/年).
(千克/年).
(1)当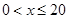 时,求函数
时,求函数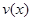 的表达式;
的表达式;
(2)当养殖密度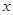 为多大时,鱼的年生长量(单位:千克/立方米)
为多大时,鱼的年生长量(单位:千克/立方米)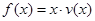 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.
推荐套卷
“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度 (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度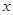 (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当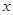 不超过4(尾/立方米)时,
不超过4(尾/立方米)时, 的值为
的值为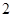 (千克/年);当
(千克/年);当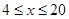 时,
时, 是
是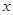 的一次函数;当
的一次函数;当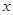 达到
达到 (尾/立方米)时,因缺氧等原因,
(尾/立方米)时,因缺氧等原因, 的值为
的值为 (千克/年).
(千克/年).
(1)当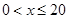 时,求函数
时,求函数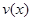 的表达式;
的表达式;
(2)当养殖密度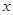 为多大时,鱼的年生长量(单位:千克/立方米)
为多大时,鱼的年生长量(单位:千克/立方米)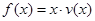 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.