如图，在四棱锥ABCD-PGFE中，底面ABCD是直角梯形，侧棱垂直于底面，AB//DC，∠ABC＝45o，DC＝1，AB＝2，PA＝1．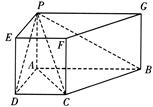
（Ⅰ）求PD与BC所成角的大小；
（Ⅱ）求证：BC⊥平面PAC；
（Ⅲ）求二面角A-PC-D的大小．
，记
，已知定义域为
的函数
有反函数
，且
，若方程
有解
，则
； 2)
的奇偶性和单调性（不要求给出证明）；
的值域为
，求实数
的取值范围
；
在
上是增函数；
推荐套卷
如图，在四棱锥ABCD-PGFE中，底面ABCD是直角梯形，侧棱垂直于底面，AB//DC，∠ABC＝45o，DC＝1，AB＝2，PA＝1．
（Ⅰ）求PD与BC所成角的大小；
（Ⅱ）求证：BC⊥平面PAC；
（Ⅲ）求二面角A-PC-D的大小．
粤公网安备 44130202000953号