如图，在△ABC中，∠BAC＝90°，AB＝AC＝6，D为BC的中点．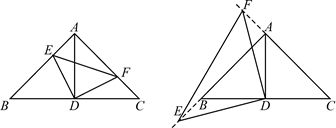
（1）若E、F分别是AB、AC上的点，且AE＝CF，求证：△AED≌△CFD；
（2）当点F、E分别从C、A两点同时出发，以每秒1个单位长度的速度沿CA、AB运动，到点A、B时停止；设△DEF的面积为y，F点运动的时间为x，求y与x的函数关系式；
（3）在（2）的条件下，点F、E分别沿CA、AB的延长线继续运动，求此时y与x的函数关系式．
相关试题
如图，已知等腰△AOB放置在平面直角坐标系xOy中， OA=OB，点B的坐标为（3，4）．
（1）求直线AB的解析式；
（2）问将等腰△AOB沿x轴正方向平移多少个单位，能使点B落在反比例函数
（x＞0）的图象上．
，其中m是方程
的根
的最小整数解．
相关知识点
推荐套卷
粤公网安备 44130202000953号