设椭圆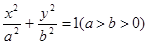 的左焦点为
的左焦点为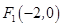 ,直线
,直线 与
与 轴交于点
轴交于点 ,过点
,过点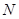 且倾斜角为30°的直线
且倾斜角为30°的直线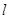 交椭圆于
交椭圆于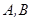 两点.
两点.
(Ⅰ)求直线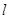 和椭圆的方程;
和椭圆的方程;
(Ⅱ)求证:点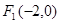 在以线段
在以线段 为直径的圆上;
为直径的圆上;
(Ⅲ)在直线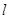 上有两个不重合的动点
上有两个不重合的动点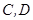 ,以
,以 为直径且过点
为直径且过点 的所有圆中,求面积最小的圆的半径长.
的所有圆中,求面积最小的圆的半径长.
推荐套卷
设椭圆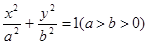 的左焦点为
的左焦点为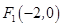 ,直线
,直线 与
与 轴交于点
轴交于点 ,过点
,过点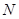 且倾斜角为30°的直线
且倾斜角为30°的直线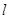 交椭圆于
交椭圆于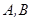 两点.
两点.
(Ⅰ)求直线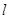 和椭圆的方程;
和椭圆的方程;
(Ⅱ)求证:点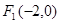 在以线段
在以线段 为直径的圆上;
为直径的圆上;
(Ⅲ)在直线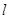 上有两个不重合的动点
上有两个不重合的动点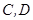 ,以
,以 为直径且过点
为直径且过点 的所有圆中,求面积最小的圆的半径长.
的所有圆中,求面积最小的圆的半径长.