四名教师被分到甲、乙、丙三所学校参加工作，每所学校至少一名教师．
（Ⅰ）求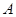
、
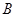两名教师被同时分配到甲学校的概率；
（Ⅱ）求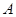、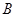两名教师不在同一学校的概率；
（Ⅲ）设随机变量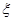
为这四名教师中分配到甲学校的人数，求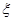的分布列和数学期望．
的函数
是奇函数．
的值；
，不等式
恒成立，求
的取值范围.
与圆
相交于
两点，并且
，求实数
的值.
，若
，且
，证明：
.
.
若函数
的最小值是
，求
的值；
用定义证明函数
在定义域上是增函数.
.
，求满足
的概率；
，求满足推荐套卷
四名教师被分到甲、乙、丙三所学校参加工作，每所学校至少一名教师．
（Ⅰ）求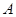、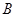两名教师被同时分配到甲学校的概率；
（Ⅱ）求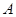、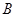两名教师不在同一学校的概率；
（Ⅲ）设随机变量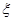为这四名教师中分配到甲学校的人数，求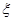的分布列和数学期望．
粤公网安备 44130202000953号