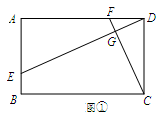
已知四边形ABCD中，E、F分别是AB、AD边上的点，DE与CF交于点G．
（1）如图①，若四边形ABCD是矩形，且DE⊥CF，求证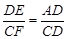
； 
（2）如图②，若四边形ABCD是平行四边形，试探究：当∠B与∠EGC满足什么关系时，使得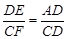成立？并证明你的结论；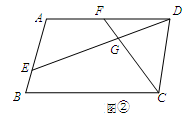 
（3）如图③，若BA=BC=6，DA=DC=8，∠BAD＝90°，DE⊥CF，请直接写出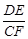
的值．
相关试题
．
，再选择一个恰当的x值代入并求值．
．
与
轴交于点
，与
轴交于点A、B，点A的坐标为（4，0）
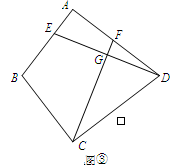
相关知识点
推荐套卷
已知四边形ABCD中，E、F分别是AB、AD边上的点，DE与CF交于点G．
（1）如图①，若四边形ABCD是矩形，且DE⊥CF，求证；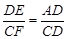
（2）如图②，若四边形ABCD是平行四边形，试探究：当∠B与∠EGC满足什么关系时，使得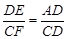成立？并证明你的结论；
（3）如图③，若BA=BC=6，DA=DC=8，∠BAD＝90°，DE⊥CF，请直接写出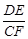的值．
粤公网安备 44130202000953号