已知：四棱锥P—ABCD的底面为直角梯形，且AB∥CD，∠DAB＝90o，DC＝2AD＝2AB，侧面PAD与底面垂直，PA＝PD，点M为侧棱PC上一点．
（1）若PA＝AD，求PB与平面PAD的所成角大小；
（2）问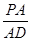
多大时，AM⊥平面PDB可能成立？
相关试题
，
，若
，求实数a的取值范围
（
为常数），
的图象与
轴有唯一的交点，求
，
]为单调函数，求
满足
，
的解析式；
上的单调性推荐套卷
已知：四棱锥P—ABCD的底面为直角梯形，且AB∥CD，∠DAB＝90o，DC＝2AD＝2AB，侧面PAD与底面垂直，PA＝PD，点M为侧棱PC上一点．
（1）若PA＝AD，求PB与平面PAD的所成角大小；
（2）问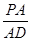多大时，AM⊥平面PDB可能成立？
粤公网安备 44130202000953号