如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.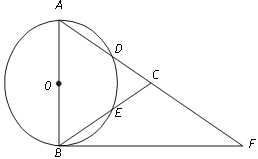
(1)求证:直线BF是⊙O的切线;
(2)若点D,点E分别是弧AB的三等分点,当AD=5时,求BF的长和扇形DOE的面积;
(3)在(2)的条件下,如果以点C为圆心,r为半径的圆上总存在不同的两点到点O的距离为5,则r的取值范围为 .
相关知识点
推荐套卷
如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.
(1)求证:直线BF是⊙O的切线;
(2)若点D,点E分别是弧AB的三等分点,当AD=5时,求BF的长和扇形DOE的面积;
(3)在(2)的条件下,如果以点C为圆心,r为半径的圆上总存在不同的两点到点O的距离为5,则r的取值范围为 .