2012年10月莫言获得诺贝尔文学奖后,其家乡山东高密政府准备投资6.7亿元打造旅游带,包括莫言旧居周围的莫言文化体验区,红高粱文化休闲区,爱国主义教育基地等;为此某文化旅游公司向社会公开征集旅游带建设方案,在收到的方案中甲、乙、丙三个方案引起了专家评委的注意,现已知甲、乙、丙三个方案能被选中的概率分别为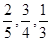 ,且假设各自能否被选中是无关的.
,且假设各自能否被选中是无关的.
(1)求甲、乙、丙三个方案只有两个被选中的概率;
(2)记甲、乙、丙三个方案被选中的个数为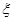 ,试求
,试求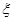 的期望.
的期望.
相关知识点
推荐套卷
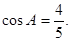
 的值;(2)若
的值;(2)若 的值。
的值。
 图象的对称中心的横坐标;
图象的对称中心的横坐标; ,求函数
,求函数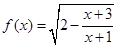 的定义域为集合A,函数
的定义域为集合A,函数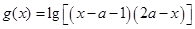 的定义域为集合B.
的定义域为集合B. A,求实数
A,求实数 的取值范围。
的取值范围。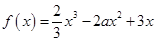 (
( ).
). 的单调区间;
的单调区间; 在
在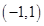 内有且只有一个极值点, 求a的取值范围.
内有且只有一个极值点, 求a的取值范围.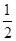 ,一个焦点是F(0,1).
,一个焦点是F(0,1).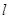 过点F交椭圆于A、B两点,且
过点F交椭圆于A、B两点,且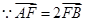 ,求直线
,求直线 粤公网安备 44130202000953号
粤公网安备 44130202000953号