运货卡车以每小时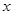
千米的速度匀速行驶130千米
（单位：千米/小时）．假设汽油的价格是每升2元，而汽车每小时耗油
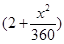升，司机的工资是每小时14元.
（Ⅰ）求这次行车总费用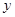
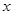关于的表达式；
（Ⅱ）当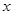为何值时，这次行车的总费用最低，并求出最低费用的值．
终边上一点
，
．
的值；
的值．
．
，求
的值；
对于
恒成立，求实数
的取值范围．
的定义域是
，对定义域内的任意
都有
，且当
；
推荐套卷
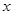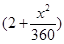运货卡车以每小时千米的速度匀速行驶130千米（单位：千米/小时）．假设汽油的价格是每升2元，而汽车每小时耗油升，司机的工资是每小时14元.
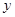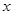（Ⅰ）求这次行车总费用关于的表达式；
（Ⅱ）当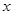为何值时，这次行车的总费用最低，并求出最低费用的值．
粤公网安备 44130202000953号