在极坐标系内，已知曲线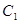
的方程为
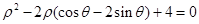，以极点为原点，极轴方向为
正半轴方向，利用相同单位长度建立平面直角坐标系，曲线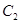
的参数方程为
（
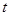为参数）.
(1)求曲线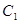的直角坐标方程以及曲线
的普通方程；
(2)设点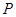
为曲线上的动点，过点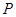作曲线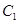
的两条切线，求这两条切线所成角余弦值的取值范围.
相关试题
中，
，
，
， M是A1B1的中点
；
与
所成角的余弦值
，
.
求
的值;（2）设
求
的最小值。
的前
项和为
, 已知
.
和公差
的值;（Ⅱ）若
，求
在
上为增函数．推荐套卷
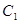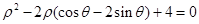在极坐标系内，已知曲线的方程为，以极点为原点，极轴方向为正半轴方向，利用相同单位长度建立平面直角坐标系，曲线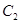的参数方程为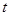（为参数）.
(1)求曲线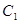的直角坐标方程以及曲线的普通方程；
(2)设点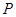为曲线上的动点，过点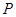作曲线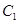的两条切线，求这两条切线所成角余弦值的取值范围.
粤公网安备 44130202000953号