已知圆
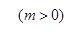 与抛物线
与抛物线 相交于
相交于 ,
, 两点
两点
(Ⅰ)求圆 的半径,抛物线的焦点坐标及准线方程;
的半径,抛物线的焦点坐标及准线方程;
(Ⅱ)设 是抛物线上不同于
是抛物线上不同于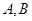 的点,且在圆外部,
的点,且在圆外部, 的延长线交圆于点
的延长线交圆于点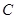 ,直线
,直线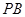 与
与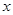 轴交于点
轴交于点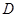 ,点
,点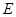 在直线
在直线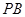 上,且四边形
上,且四边形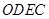 为等腰梯形,求点
为等腰梯形,求点 的坐标.
的坐标.
推荐套卷
已知圆
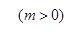 与抛物线
与抛物线 相交于
相交于 ,
, 两点
两点
(Ⅰ)求圆 的半径,抛物线的焦点坐标及准线方程;
的半径,抛物线的焦点坐标及准线方程;
(Ⅱ)设 是抛物线上不同于
是抛物线上不同于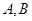 的点,且在圆外部,
的点,且在圆外部, 的延长线交圆于点
的延长线交圆于点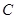 ,直线
,直线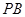 与
与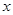 轴交于点
轴交于点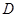 ,点
,点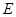 在直线
在直线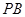 上,且四边形
上,且四边形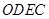 为等腰梯形,求点
为等腰梯形,求点 的坐标.
的坐标.