已知动点 到点
到点 的距离与到直线
的距离与到直线 的距离之比为定值
的距离之比为定值 ,记
,记 的轨迹为
的轨迹为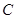 .
.
(1)求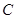 的方程,并画出
的方程,并画出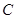 的简图;
的简图;
(2)点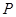 是圆
是圆 上第一象限内的任意一点,过
上第一象限内的任意一点,过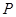 作圆的切线交轨迹
作圆的切线交轨迹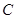 于
于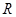 ,
, 两点.
两点.
(i)证明: ;
;
(ii)求 的最大值.
的最大值.
推荐套卷
已知动点 到点
到点 的距离与到直线
的距离与到直线 的距离之比为定值
的距离之比为定值 ,记
,记 的轨迹为
的轨迹为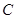 .
.
(1)求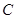 的方程,并画出
的方程,并画出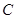 的简图;
的简图;
(2)点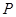 是圆
是圆 上第一象限内的任意一点,过
上第一象限内的任意一点,过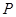 作圆的切线交轨迹
作圆的切线交轨迹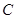 于
于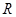 ,
, 两点.
两点.
(i)证明: ;
;
(ii)求 的最大值.
的最大值.