如图,小敏、小亮从A,B两地观测空中C处一个气球,分别测得仰角为30°和60°,A,B两地相距100 米.当气球沿与BA平行地飘移10秒后到达C′处时,在A处测得气球的仰角为45°.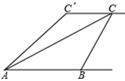
(1)求气球的高度(结果精确到0.1米);
(2)求气球飘移的平均速度(结果保留3个有效数字).
相关知识点
推荐套卷
如图,小敏、小亮从A,B两地观测空中C处一个气球,分别测得仰角为30°和60°,A,B两地相距100 米.当气球沿与BA平行地飘移10秒后到达C′处时,在A处测得气球的仰角为45°.
(1)求气球的高度(结果精确到0.1米);
(2)求气球飘移的平均速度(结果保留3个有效数字).