已知函数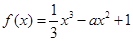
．
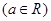（Ⅰ）若曲线y=f(x)在(1，f(1))处的切线与直线x+y+1=0平行，求a的值；
（Ⅱ）若a>0，函数y=f(x)在区间(a，a 2-3)上存在极值，求a的取值范围；
（Ⅲ）若a>2，求证：函数y=f(x)在(0，2)上恰有一个零点．
的最大值和最小值
是实数，
，试证明：对于任意
在
上为增函数
SA＝{a＋3}，求a的值．推荐套卷
已知函数 ．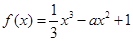
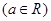（Ⅰ）若曲线y=f(x)在(1，f(1))处的切线与直线x+y+1=0平行，求a的值；
（Ⅱ）若a>0，函数y=f(x)在区间(a，a 2-3)上存在极值，求a的取值范围；
（Ⅲ）若a>2，求证：函数y=f(x)在(0，2)上恰有一个零点．
粤公网安备 44130202000953号