某项竞赛分别为初赛、复赛、决赛三个阶段进行，每个阶段选手要回答一个问题.规定正确回答问题者进入下一阶段竞赛，否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是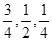
，且各阶段通过与否相互独立.
（I）求该选手在复赛阶段被淘汰的概率；
（II）设该选手在竞赛中回答问题的个数为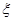
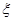，求的分布列、数学期望和方差.
相关试题
，其中
且m为常数．
时函数
在区间
上的单调性，并证明； 
在
处取得极值，求
的值，并讨论函数
．
的递减区间；
上的最值．
满足到定点
的距离与到定点
距离之比为
．
的方程；
的直线
与曲线
，若
，求直线
中，
，
，
为正三角形，且平面
平面
．
；
的余弦值．
中，角
所对的边分别为
，且
成等差数列．
的大小；
，求
边上中线长的最小值．推荐套卷
某项竞赛分别为初赛、复赛、决赛三个阶段进行，每个阶段选手要回答一个问题.规定正确回答问题者进入下一阶段竞赛，否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是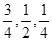，且各阶段通过与否相互独立.
（I）求该选手在复赛阶段被淘汰的概率；
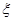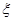（II）设该选手在竞赛中回答问题的个数为，求的分布列、数学期望和方差.
粤公网安备 44130202000953号