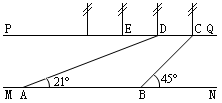
如图,宝应生态园中有一条人工河,河的两岸PQ、MN互相平行,河岸PQ上有一排间隔为50米的彩灯柱C、D、E、……,某人在河岸MN的A处测得∠DAN=21º,然后沿河岸走了175米到达B处,测得∠CBN=45º,求这条河的宽度.
(参考数据: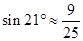 ,
,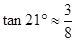 )
)
相关知识点
推荐套卷
如图,宝应生态园中有一条人工河,河的两岸PQ、MN互相平行,河岸PQ上有一排间隔为50米的彩灯柱C、D、E、……,某人在河岸MN的A处测得∠DAN=21º,然后沿河岸走了175米到达B处,测得∠CBN=45º,求这条河的宽度.
(参考数据: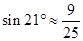 ,
,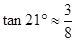 )
)