(本题12分)如图,抛物线 交
交 轴正半轴于点A,顶点为M,对称轴NB交
轴正半轴于点A,顶点为M,对称轴NB交 轴于点B,过点C(2,0)作射线CD交MB于点D(D在
轴于点B,过点C(2,0)作射线CD交MB于点D(D在 轴上方),OE∥CD交MB于点E,EF∥
轴上方),OE∥CD交MB于点E,EF∥ 轴交CD于点F,作直线MF。
轴交CD于点F,作直线MF。
(1)求点A,M的坐标;
(2)当BD为何值时,点F恰好落在抛物线上?
(3)当BD=1时,①、求直线MF的解析式,并判断点A是否落在该直线上;
②、延长OE交FM于点G,取CF中点P,连结PG,△FPG,四边形DEGP,四边形OCDE的面积分别记为S1,S2,S3,则S1:S2:S3=
相关知识点
推荐套卷
 ,点B、C、D在直线l上,按下列要求画图(保留画图痕迹);
,点B、C、D在直线l上,按下列要求画图(保留画图痕迹);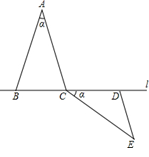
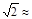 1.414,
1.414,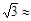 1.732)
1.732)
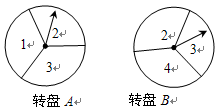
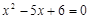 的解”时,王磊得1分;若“两个指针所指的数字都不是方程
的解”时,王磊得1分;若“两个指针所指的数字都不是方程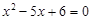 的解”时,张浩得3分,这个游戏公平吗?为什么?
的解”时,张浩得3分,这个游戏公平吗?为什么?
 粤公网安备 44130202000953号
粤公网安备 44130202000953号