在一次测量旗杆高度的活动中,某小组使用的方案如下:
如图,AB表示某同学从眼睛到脚底的距离,CD表示一根标杆,EF表示旗杆,AB、CD、EF都垂直于地面,若AB=1.6m,CD=2m,人与标杆之间的距离BD=1m,标杆与旗杆之间的距离DF=30m,求旗杆EF的高度.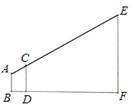
相关知识点
推荐套卷
在一次测量旗杆高度的活动中,某小组使用的方案如下:
如图,AB表示某同学从眼睛到脚底的距离,CD表示一根标杆,EF表示旗杆,AB、CD、EF都垂直于地面,若AB=1.6m,CD=2m,人与标杆之间的距离BD=1m,标杆与旗杆之间的距离DF=30m,求旗杆EF的高度.