如图,在平面直角坐标系中,点A的坐标为(7,0),点B的坐标为(3,4),
(1)求经过O、A、B三点的抛物线解析式;
(2)将线段AB绕A点顺时针旋转75°至AC,直接写出点C的坐标.
(3)在y轴上找一点P,第一象限找一点Q,使得以O、B、Q、P为顶点的四边形是菱形,求出点Q的坐标;
(4)△OAB的边OB上有一动点M,过M作MN//OA交AB于N,将△BMN沿MN翻折得△DMN,设MN=x,△DMN与△OAB重叠部分的面积为y,求出y与x之间的函数关系式,并求出重叠部分面积的最大值.
相关知识点
推荐套卷
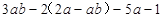 ,其中
,其中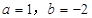
 -1.
-1. ―
―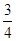 +
+ )
)
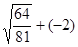

 ,
, ,-3,
,-3, 。
。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号