某玩具由一个圆形区域和一个扇形区域组成，如图，在⊙O1和扇形O2CD中，⊙O1与O2C、O2D分别相切于A、B，∠CO2D=60°，直线O1O2与⊙O1、扇形O2CD分别交于E、F两个点，EF=24cm，设⊙O1的半径为xcm，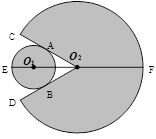
（1）用含x的代数式表示扇形O2CD的半径；
（2）若⊙O1和扇形O2CD两个区域的制作成本分别为0.45元／cm2和0.06／cm2元，当⊙O1的半径为多少时，该玩具成本最小？
m/s，求光经过7.8×10
m所需的时间(四舍五入到百分位)
相关知识点
推荐套卷
某玩具由一个圆形区域和一个扇形区域组成，如图，在⊙O1和扇形O2CD中，⊙O1与O2C、O2D分别相切于A、B，∠CO2D=60°，直线O1O2与⊙O1、扇形O2CD分别交于E、F两个点，EF=24cm，设⊙O1的半径为xcm，
（1）用含x的代数式表示扇形O2CD的半径；
（2）若⊙O1和扇形O2CD两个区域的制作成本分别为0.45元／cm2和0.06／cm2元，当⊙O1的半径为多少时，该玩具成本最小？
粤公网安备 44130202000953号