如图，在矩形ABCD中，AD=4，M是AD的中点，点E是线段AB上一动点，连接EM并延长交线段CD的延长线于点F．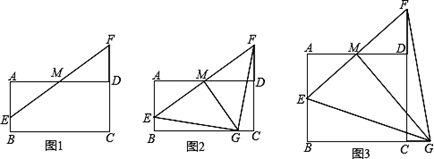
（1）如图1，求证：AE=DF；
（2）如图2，若AB=2，过点M作 MG⊥EF交线段BC于点G，求证：△GEF是等腰直角三角形
（3）如图3，若AB=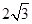
，过点M作 MG⊥EF交线段BC的延长线于点G．
①直接写出线段AE长度的取值范围；
②判断△GEF的形状，并说明理由．
，其中
．
）÷
，其中的x选一个适当的数代入求值．
的两根，求
的值．
，其中
．
，请选取一个适当的x的数值代入求值．相关知识点
推荐套卷
如图，在矩形ABCD中，AD=4，M是AD的中点，点E是线段AB上一动点，连接EM并延长交线段CD的延长线于点F．
（1）如图1，求证：AE=DF；
（2）如图2，若AB=2，过点M作 MG⊥EF交线段BC于点G，求证：△GEF是等腰直角三角形
（3）如图3，若AB=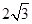，过点M作 MG⊥EF交线段BC的延长线于点G．
①直接写出线段AE长度的取值范围；
②判断△GEF的形状，并说明理由．
粤公网安备 44130202000953号