如图,防洪大堤的横断面是梯形,背水坡AB的坡度i=1: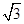 ,且AB=20m.身高为1.7m的小明站在大堤A点,测得髙压电线杆顶端点D的仰角为30°.已知地面CB宽30m,求小明到电线杆的距离和髙压电线杆CD的髙度(结果保留根号).
,且AB=20m.身高为1.7m的小明站在大堤A点,测得髙压电线杆顶端点D的仰角为30°.已知地面CB宽30m,求小明到电线杆的距离和髙压电线杆CD的髙度(结果保留根号).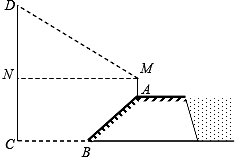
相关知识点
推荐套卷
如图,防洪大堤的横断面是梯形,背水坡AB的坡度i=1: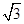 ,且AB=20m.身高为1.7m的小明站在大堤A点,测得髙压电线杆顶端点D的仰角为30°.已知地面CB宽30m,求小明到电线杆的距离和髙压电线杆CD的髙度(结果保留根号).
,且AB=20m.身高为1.7m的小明站在大堤A点,测得髙压电线杆顶端点D的仰角为30°.已知地面CB宽30m,求小明到电线杆的距离和髙压电线杆CD的髙度(结果保留根号).